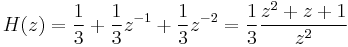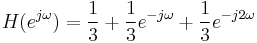Finite impulse response
A finite impulse response (FIR) filter is a type of a signal processing filter whose impulse response (or response to any finite length input) is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response of an Nth-order discrete-time FIR filter (i.e. with a Kronecker delta impulse input) lasts for N+1 samples, and then dies to zero.
FIR filters can be discrete-time or continuous-time, and digital or analog.
Contents |
Definition
The output y of a linear time invariant system is determined by convolving its input signal x with its impulse response b.
For a discrete-time FIR filter, the output is a weighted sum of the current and a finite number of previous values of the input. The operation is described by the following equation, which defines the output sequence y[n] in terms of its input sequence x[n]:
where:
![x[n]](/2012-wikipedia_en_all_nopic_01_2012/I/d3baaa3204e2a03ef9528a7d631a4806.png) is the input signal,
is the input signal,![y[n]](/2012-wikipedia_en_all_nopic_01_2012/I/a39037ba03412351ec1f3c8ca9e807fd.png) is the output signal,
is the output signal,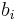 are the filter coefficients, also known as tap weights, that make up the impulse response,
are the filter coefficients, also known as tap weights, that make up the impulse response, is the filter order; an
is the filter order; an  th-order filter has
th-order filter has 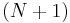 terms on the right-hand side. The
terms on the right-hand side. The ![x[n-i]](/2012-wikipedia_en_all_nopic_01_2012/I/38f5da83071a58feac909a851da83ae0.png) in these terms are commonly referred to as taps, based on the structure of a tapped delay line that in many implementations or block diagrams provides the delayed inputs to the multiplication operations. One may speak of a "5th order/6-tap filter", for instance.
in these terms are commonly referred to as taps, based on the structure of a tapped delay line that in many implementations or block diagrams provides the delayed inputs to the multiplication operations. One may speak of a "5th order/6-tap filter", for instance.
Properties
An FIR filter has a number of useful properties which sometimes make it preferable to an infinite impulse response (IIR) filter. FIR filters:
- Require no feedback. This means that any rounding errors are not compounded by summed iterations. The same relative error occurs in each calculation. This also makes implementation simpler.
- Are inherently stable. This is due to the fact that, because there is no required feedback, all the poles are located at the origin and thus are located within the unit circle (the required condition for stability in a Z transformed system).
- They can easily be designed to be linear phase by making the coefficient sequence symmetric; linear phase, or phase change proportional to frequency, corresponds to equal delay at all frequencies. This property is sometimes desired for phase-sensitive applications, for example data communications, crossover filters, and mastering.
The main disadvantage of FIR filters is that considerably more computation power in a general purpose processor is required compared to an IIR filter with similar sharpness or selectivity, especially when low frequency (relative to the sample rate) cutoffs are needed. However many digital signal processors provide specialized hardware features to make FIR filters approximately as efficient as IIR for many applications.
Impulse response
The impulse response ![h[n]](/2012-wikipedia_en_all_nopic_01_2012/I/76df30cb2f3c2675e057e25429917f27.png) can be calculated if we set
can be calculated if we set ![\ x[n] = \delta[n]](/2012-wikipedia_en_all_nopic_01_2012/I/28f280744d077339a36da5dd6bb2c369.png) in the above relation, where
in the above relation, where ![\delta[n]](/2012-wikipedia_en_all_nopic_01_2012/I/975c0ff50f5aebd603d5da0602b0f31d.png) is the Kronecker delta impulse. The impulse response for an FIR filter then becomes the set of coefficients
is the Kronecker delta impulse. The impulse response for an FIR filter then becomes the set of coefficients 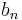 , as follows
, as follows
for 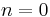 to
to 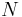 .
.
The Z-transform of the impulse response yields the transfer function of the FIR filter
FIR filters are clearly bounded-input bounded-output (BIBO) stable, since the output is a sum of a finite number of finite multiples of the input values, so can be no greater than 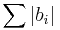 times the largest value appearing in the input.
times the largest value appearing in the input.
Filter design
To design a filter means to select the coefficients such that the system has specific characteristics. The required characteristics are stated in filter specifications. Most of the time filter specifications refer to the frequency response of the filter. There are different methods to find the coefficients from frequency specifications:
- Window design method
- Frequency Sampling method
- Weighted least squares design
- Parks-McClellan method (also known as the Equiripple, Optimal, or Minimax method). The Remez exchange algorithm is commonly used to find an optimal equiripple set of coefficients. Here the user specifies a desired frequency response, a weighting function for errors from this response, and a filter order N. The algorithm then finds the set of
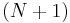 coefficients that minimize the maximum deviation from the ideal. Intuitively, this finds the filter that is as close as you can get to the desired response given that you can use only
coefficients that minimize the maximum deviation from the ideal. Intuitively, this finds the filter that is as close as you can get to the desired response given that you can use only 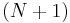 coefficients. This method is particularly easy in practice since at least one text[1] includes a program that takes the desired filter and N, and returns the optimum coefficients.
coefficients. This method is particularly easy in practice since at least one text[1] includes a program that takes the desired filter and N, and returns the optimum coefficients. - Equiripple FIR filters can be designed using the FFT algorithms as well[2]. The algorithm is iterative in nature. You simply compute the DFT of an initial filter design that you have using the FFT algorithm (if you don't have an initial estimate you can start with h[n]=delta[n]). In the Fourier domain or FFT domain you correct the frequency response according to your desired specs and compute the inverse FFT. In time-domain you retain only N of the coefficients (force the other coefficients to zero). Compute the FFT once again. Correct the frequency response according to specs.
Software packages like MATLAB, GNU Octave, Scilab, and SciPy provide convenient ways to apply these different methods.
Some filter specifications refer to the time-domain shape of the input signal the filter is expected to "recognize". The optimum matched filter for separating any waveform from white noise is obtained by sampling that shape and using those samples in reverse order as the coefficients of the filter -- giving the filter an impulse response that is the time-reverse of the expected input signal.
Window design method
In the Window Design Method, one designs an ideal IIR filter, then applies a window function to it – in the time domain, multiplying the infinite impulse by the window function. This results in the frequency response of the IIR being convolved with the frequency response of the window function. If the ideal response is sufficiently simple, such as rectangular, the result of the convolution can be relatively easy to determine. In fact one usually specifies the desired result first and works backward to determine the appropriate window function parameter(s). Kaiser windows are particularly well-suited for this method because of their closed form specifications.
Moving average example
A moving average filter is a very simple FIR filter. It is sometimes called a boxcar filter, especially when followed by decimation. The filter coefficients are found via the following equation:
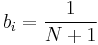 for
for 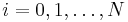
To provide a more specific example, we select the filter order:
The impulse response of the resulting filter is:
The Fig. (a) on the right shows the block diagram of a 2nd-order moving-average filter discussed below. To discuss stability and spectral topics we take the z-transform of the impulse response:
Fig. (b) on the right shows the pole-zero diagram of the filter. Zero frequency (DC) corresponds to (1,0), positive frequencies advancing counterclockwise around the circle to (-1,0) at half the sample frequency. Two poles are located at the origin, and two zeros are located at 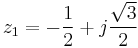 ,
, 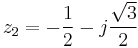
The frequency response, for frequency ω in radians per sample, is:
Fig. (c) on the right shows the magnitude and phase plots of the frequency response. Clearly, the moving-average filter passes low frequencies with a gain near 1, and attenuates high frequencies. This is a typical low-pass filter characteristic. Frequencies above π are aliases of the frequencies below π, and are generally ignored or filtered out if reconstructing a continuous-time signal. The following figure shows the phase response. Since the phase always follows a straight line except where it has been reduced modulo π radians (should be 2π), the linear phase property is demonstrated.
See also
- Electronic filter
- Filter (signal processing)
- Infinite impulse response (IIR) filter
- Z-transform (specifically Linear constant-coefficient difference equation)
- Filter design
- Cascaded Integrator-Comb Filter
- Compact support
References
- ^ Rabiner, Lawrence R., and Gold, Bernard, 1975: Theory and Application of Digital Signal Processing (Englewood Cliffs, New Jersey: Prentice-Hall, Inc.) ISBN 0139141014
- ^ A. E. Cetin, O.N. Gerek, Y. Yardimci, "Equiripple FIR filter design by the FFT algorithm," IEEE Signal Processing Magazine, pp. 60-64, March 1997.
External links
- Notes on the Optimal Design of FIR Filters Connexions online book by John Treichler (2008).
- FIR FAQ provided by dspguru.com.
- BruteFIR; Software for applying long FIR filters to multi-channel digital audio, either offline or in realtime.
- Freeverb3 Reverb Impulse Response Processor
- FIR filter design
- An n-tap FIR filter written in VHDL
- Worked examples and explanation for designing FIR filters using windowing. Includes code examples.
- A JAVA applet with different FIR-filters; the filters are applied to sound and the results can be heard immediately. The source code is also available.
- Matlab code; Matlab code for "Equiripple FIR filter design by the FFT algorithm" by A. Enis Cetin, O. N. Gerek and Y. Yardimci, IEEE Signal Processing Magazine, 1997.
![y[n]=b_0 x[n] %2B b_1 x[n-1] %2B \cdots %2B b_N x[n-N]](/2012-wikipedia_en_all_nopic_01_2012/I/86a07c0e0e1b5328054621a97b8a1199.png)
![y[n] = \sum_{i=0}^{N} b_i x[n-i]](/2012-wikipedia_en_all_nopic_01_2012/I/f529cdc0903f73eec3e31f275ff5da4f.png)
![\begin{align}
h[n] &= \sum_{i=0}^{N}b_i \delta[n-i] \\
&= b_n.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/5da1b6004b16da6423019b0a248a64e3.png)
![\begin{align}
H(z) &= Z\{h[n]\} \\
&= \sum_{n=-\infty}^{\infty} h[n] z^{-n} \\
&= \sum_{n=0}^{N}b_n\,z^{-n}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/301ce6314cadbaee085e64a540e57609.png)
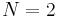
![h[n]=\frac{1}{3}\delta[n]%2B\frac{1}{3}\delta[n-1]%2B\frac{1}{3}\delta[n-2]](/2012-wikipedia_en_all_nopic_01_2012/I/1624bc7c4352ab7f8b541abd9b83012f.png)